矩阵设置

矩阵是数学中的一种矩形数组，用于表示和处理线性变换、线性方程组等，矩阵的基本操作包括加法、减法、标量乘法和矩阵乘法，下面我们详细讲解这些基本操作。

1. 矩阵的定义

一个 ( m times n ) 的矩阵是一个由 ( m ) 行 ( n ) 列元素排列成的矩形阵列，通常用大写字母表示，一个 ( 2 times 3 ) 的矩阵可以表示为：

[ A = begin{pmatrix}

a_{11} & a_{12} & a_{13}

a_{21} & a_{22} & a_{23}

end{pmatrix} ]

2. 矩阵的加法与减法

两个同型矩阵（即行数和列数相同的矩阵）可以进行加法和减法运算，假设有两个 ( m times n ) 的矩阵 ( A ) 和 ( B )，它们的加法和减法定义如下：

[ (A + B)_{ij} = A_{ij} + B_{ij} ]

[ (A B)_{ij} = A_{ij} B_{ij} ]

3. 标量乘法

一个矩阵 ( A ) 乘以一个标量 ( k ) 是将矩阵中的每个元素都乘以这个标量，( A ) 是一个 ( m times n ) 的矩阵，

[ (kA)_{ij} = k cdot A_{ij} ]

4. 矩阵乘法

矩阵乘法是线性代数中最重要的操作之一，两个矩阵 ( A ) 和 ( B ) 的乘积 ( AB ) 只有在 ( A ) 的列数等于 ( B ) 的行数时才有定义，( A ) 是 ( m times n ) 的矩阵，( B ) 是 ( n times p ) 的矩阵，那么它们的乘积 ( C = AB ) 是一个 ( m times p ) 的矩阵，其元素定义为：

[ C_{ij} = sum_{k=1}^{n} A_{ik} B_{kj} ]

5. 矩阵的转置

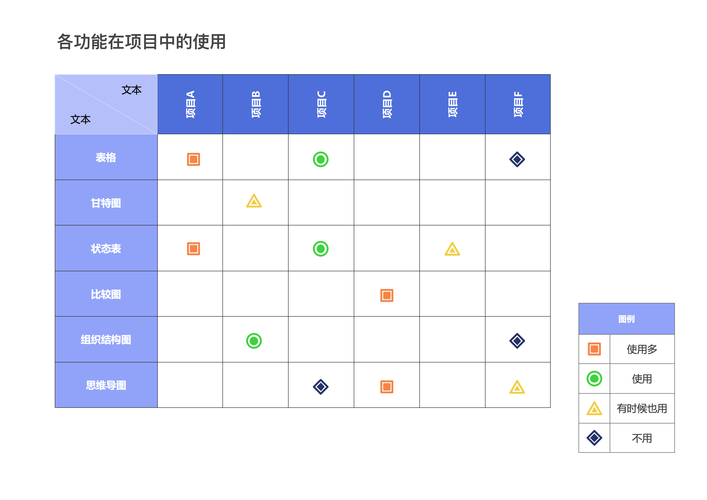
矩阵 ( A ) 的转置记作 ( A^T )，是将矩阵的行和列互换得到的新矩阵，( A ) 是一个 ( m times n ) 的矩阵，( A^T ) 是一个 ( n times m ) 的矩阵，其元素定义为：

[ (A^T)_{ij} = A_{ji} ]

6. 单位矩阵与逆矩阵

单位矩阵 ( I ) 是一个对角线上全为1，其余元素全为0的方阵，对于一个可逆矩阵 ( A )，存在一个矩阵 ( A^{-1} ) 使得：

[ AA^{-1} = A^{-1}A = I ]

7. 矩阵的行列式

行列式是一个与方阵相关的标量，用于判断矩阵是否可逆，一个 ( n times n ) 的矩阵 ( A ) 的行列式记作 ( det(A) )，( det(A) neq 0 )，则矩阵 ( A ) 是可逆的。

8. 矩阵的应用

矩阵在许多领域有广泛应用，如物理学中的量子力学、计算机科学中的图像处理、经济学中的投入产出模型等。

通过以上内容，我们了解了矩阵的基本概念和操作，希望这对你理解矩阵有所帮助。